Rotating double gyre

Tip

This example is also available as a Jupyter notebook: rot_double_gyre.ipynb, and as an executable julia file rot_double_gyre.jl.

Description

The rotating double gyre model was introduced by Mosovsky & Meiss. It can be derived from the stream function

\[\psi(x,y,t)=(1−s(t))\psi_P +s(t)\psi_F \\ \psi_P (x, y) = \sin(2\pi x) \sin(\pi y) \\ \psi_F (x, y) = \sin(\pi x) \sin(2\pi y)\]

where $s$ is (usually taken to be) a cubic interpolating function satisfying $s(0) = 0$ and $s(1) = 1$. It therefore interpolates two double-gyre-type velocity fields, from horizontally to vertically arranged counter-rotating gyres. The corresponding velocity field is provided by the package and callable as rot_double_gyre.

FEM-Based Methods

The following code demonstrates how to use these methods.

using CoherentStructures, Arpack
LL, UR = (0.0, 0.0), (1.0, 1.0)
ctx, _ = regularTriangularGrid((50, 50), LL, UR)

A = x -> mean_diff_tensor(rot_double_gyre, x, [0.0, 1.0], 1.e-10, tolerance= 1.e-4)
K = assembleStiffnessMatrix(ctx, A)
M = assembleMassMatrix(ctx)
λ, v = eigs(-K, M, which=:SM);

This velocity field is given by the rot_double_gyre function. The third argument to mean_diff_tensor is a vector of time instances at which we evaluate (and subsequently average) the pullback diffusion tensors. The fourth parameter is the step size δ used for the finite-difference scheme, tolerance is passed to the ODE solver from DifferentialEquations.jl. In the above, A(x) approximates the mean diffusion tensor given by

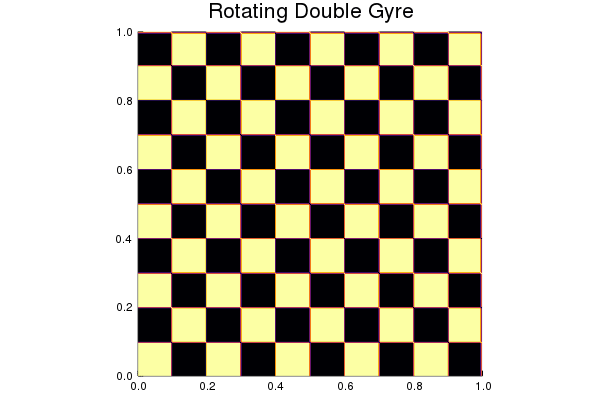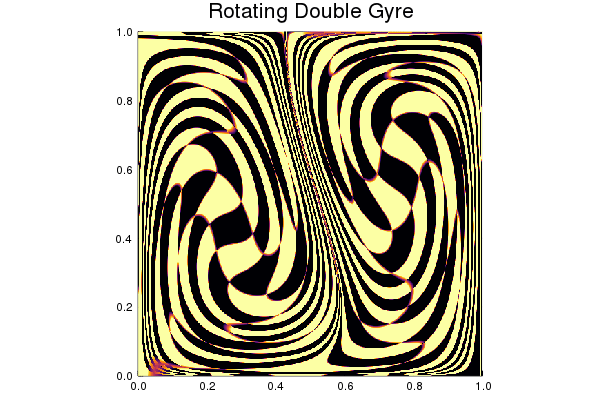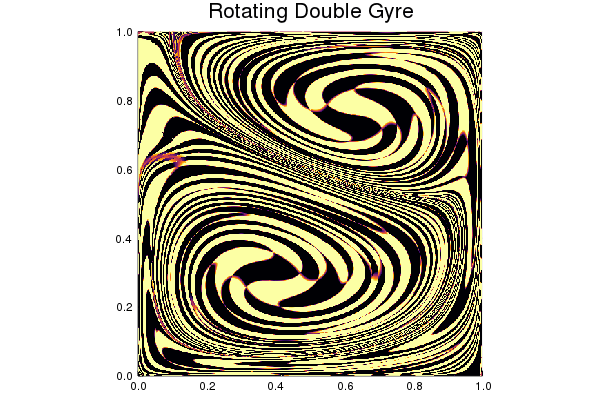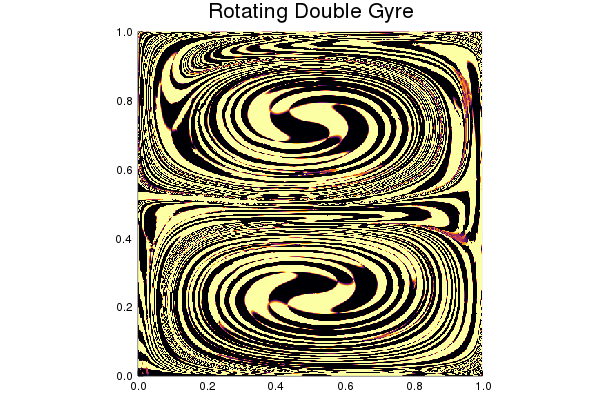
\[A(x) = \sum_{t \in \mathcal T}(D\Phi^t(x))^{-1} (D\Phi^t x)^{-T}\]

The eigenfunctions saved in v approximate those of $\Delta^{dyn}$

import Plots
res = [plot_u(ctx, v[:,i], 100, 100, colorbar=:none, clim=(-3,3)) for i in 1:6];
fig = Plots.plot(res..., margin=-10Plots.px)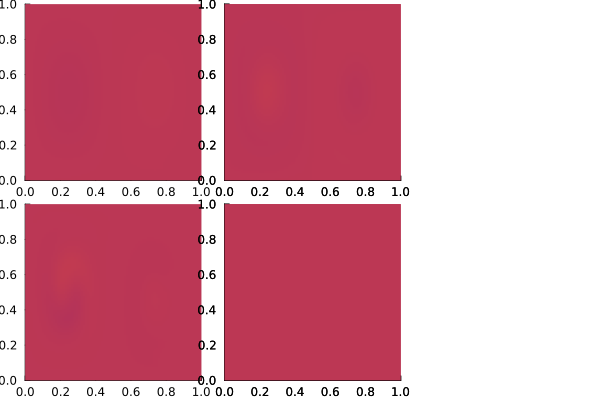

Looking at the spectrum, there appears a gap after the third eigenvalue.

spectrum_fig = Plots.scatter(1:6, real.(λ))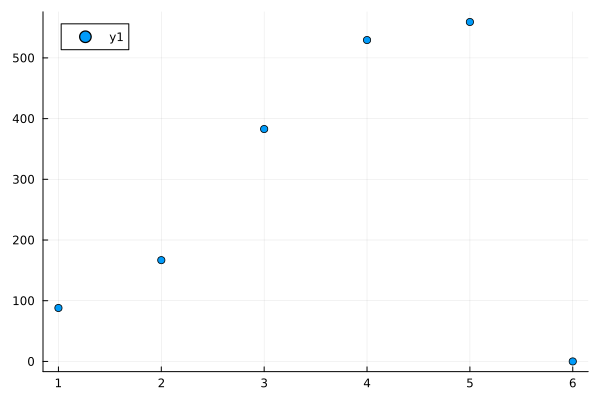

We can use the Clustering.jl package to compute coherent structures from the first two nontrivial eigenfunctions:

using Clustering

ctx2, _ = regularTriangularGrid((200, 200))
v_upsampled = sample_to(v, ctx, ctx2)

numclusters=2
res = kmeans(permutedims(v_upsampled[:,2:numclusters+1]), numclusters + 1)
u = kmeansresult2LCS(res)
res = Plots.plot([plot_u(ctx2, u[:,i], 200, 200, color=:viridis, colorbar=:none) for i in 1:3]...)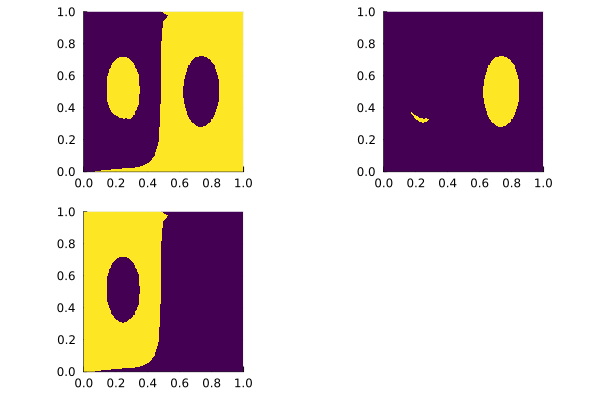

Geodesic vortices

Here, we demonstrate how to calculate black-hole vortices, see Geodesic elliptic material vortices for references and details.

using Distributed
nprocs() == 1 && addprocs()

@everywhere using CoherentStructures, OrdinaryDiffEq
using StaticArrays, AxisArrays
q = 51
tspan = range(0., stop=1., length=q)
nx = ny = 51
xmin, xmax, ymin, ymax = 0.0, 1.0, 0.0, 1.0
xspan = range(xmin, stop=xmax, length=nx)
yspan = range(ymin, stop=ymax, length=ny)
P = AxisArray(SVector{2}.(xspan, yspan'), xspan, yspan)
δ = 1.e-6
mCG_tensor = let tspan=tspan, δ=δ
    u -> av_weighted_CG_tensor(rot_double_gyre, u, tspan, δ; tolerance=1e-6, solver=Tsit5())
end

C̅ = pmap(mCG_tensor, P; batch_size=ceil(Int, length(P)/nprocs()^2))
p = LCSParameters(0.5)
vortices, singularities = ellipticLCS(C̅, p; outermost=true)

The results are then visualized as follows.

using Plots
λ₁, λ₂, ξ₁, ξ₂, traceT, detT = tensor_invariants(C̅)
fig = Plots.heatmap(xspan, yspan, permutedims(log10.(traceT));
            aspect_ratio=1, color=:viridis, leg=true,
            title="DBS field and transport barriers",
            xlims=(xmin, xmax), ylims=(ymin, ymax))
scatter!([s.coords.data for s in singularities], color=:red, label="singularities")
scatter!([vortex.center.data for vortex in vortices], color=:yellow, label="vortex cores")
for vortex in vortices, barrier in vortex.barriers
    plot!(barrier.curve, w=2, label="T = $(round(barrier.p, digits=2))")
end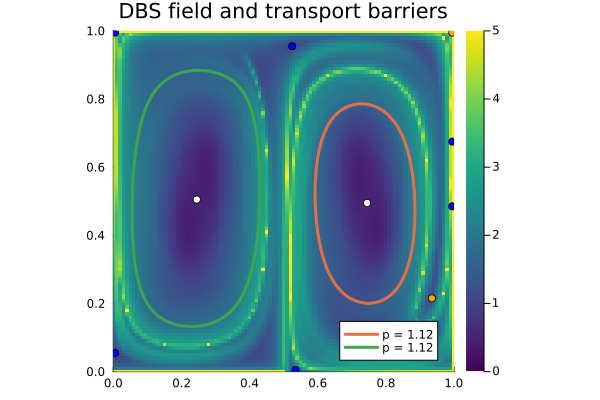

This page was generated using Literate.jl.